 Normalize Strands
Normalize Strands
Overview
Normalize Strands operator uses a hair direction normalization algorithm to de-tangle the hair strands in preparation for the simulation.

In the image above, you can see how the hair penetration is reduced or eliminated using Normalize Strands.
Parameters
Normalize Strands provides few parameters that can be adjusted to get the desired results. Additionally, those parameters can ajusted using texture maps, Strand Groups, Guide Channels and Color Sets. See the corresponding page for more information.
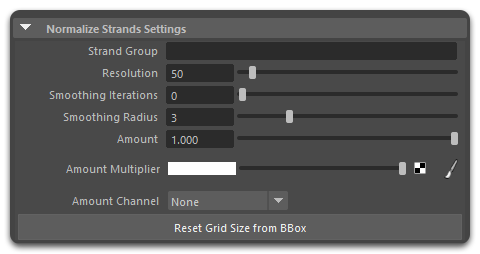
- Strand Groups
Use Strand Groups patterns to isolate the effect of this operator to certain area of the hair. - Resolution
Voxel resolution used to voxelized the hair vectors and rebuilt the hair back. With high resolution values the normalized hair strands should be nearly or identical to the original strands. With lower resolutions higher frequency detail is filtered out, and the resulting strands appear combed. At the lowest resolution (one voxel) all curves would be rebuilt going in the same direction. - Smoothing Iterations
Apply N times mean-value (i.e. box) filter of normalized directions. Normalization itself smooth strands but only with low resolutions (resolution of 1 will result in all strands having single direction). With this option strands direction could be smoothed when high resolution is used. Should provide slightly better result than using low resolutions. - Smoothing Radius
The radius of the mean-value filter used for smooth (the width of smoothing filter is 2*Radius+1 voxels). - Amount
Modulates the normalize effect. This parameter can also be controlled using Guide Channels created using the Generate Strand Data operator. - Reset Grid Size from BBox
The size of strands bounding box is used to compute voxels volume. This button could be used to update BBox after strands size change.
Related Topics
Missing Something? Let us know if this page needs more information about the topic.
Missing Something? Let us know if this page needs more information about the topic.


